Z klasické mechaniky i z běžného života víme, že hmotnost tělesa se při pohybu nemění. Jak ale bude reagovat hmotnost při rychlostech blízkých c? Isaac Newton definoval sílu jako změnu hybnosti za čas. Hybnost je součin hmotnosti a rychlosti. Jestliže by na určité těleso působila síla stálé velikosti a směru, pak se těleso dá do pohybu ve směru síly. Protože má síla konstantní velikost, pak hybnost za každou sekundu vzrůstá stejně. Podle Newtonovy mechaniky je hmotnost neměnná, proto se při zvětšování hybnosti zvětšuje rovnoměrně jen rychlost. Jestliže se síla bude zvětšovat do nekonečna, pak by se i rychlost měla zvětšovat do nekonečna. To ale podle teorie relativity není možné. Proto je nutné v Newtonově mechanice opravit úvahu o závislosti hmotnosti tělesa na rychlosti. Při působící síle se z počátku hmotnost mění nepatrně. Při zvětšující se síle se mění podstatně více. Albert Einstein ve své teorii dokázal, že hmotnost každého tělesa se s rostoucí rychlostí zvětšuje, a to podle vztahu
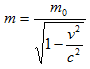
Veličina m se nazývá relativistická hmotnost, veličina m0 se nazývá klidová hmotnost. Na následujícím grafu je vidět závislost hmotnosti na rychlosti tělesa. Při malých rychlostech se hmotnost téměř nemění.
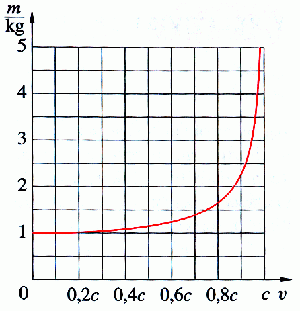
Závislost hmotnosti na rychlosti pohybu. Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Ze vztahu a obrázku plyne, že pro každé hmotné těleso je rychlost c konečná a mezní, protože po dosazení do tohoto vztahu dostáváme nekonečnou hmotnost
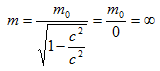
Vztah pro relativistickou hmotnost byl ověřen pomocí mnoha pokusů na urychlovačích částic. V urychlovačích se částice dají urychlit na rychlosti blízké c. Hmotnost částic se při těchto rychlostech mnohonásobně zvýší. Např. ve Stanfordu v USA urychlují částice tak, že jejich relativistická hmotnost je 40 000krát větší než klidová.
Fotony jako částice se zásadně liší od jiných látkových částic, např. elektronů nebo protonů. Fotony se ve vakuu pohybují rychlostí světla c a mají přitom nenulovou konečnou hmotnost. Podle speciální teorie relativity pro klidovou hmotnost platí
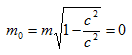
Proto říkáme, že fotony mají klidovou hmotnost nulovou.
Vzhledem k tomu, že se při rostoucí rychlosti mění hmotnost, je nutné poopravit i vztahy pro některé další veličiny s hmotností související. Podobným způsobem bychom mohli odvodit závislost dalších veličin na pohybu, např. pro hybnost platí
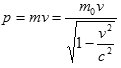
V tzv. Minkowského prostoročase má každý vektor čtyři složky – tedy i vektor hybnosti, který označujeme jako čtyřvektor hybnosti (čtyřhybnost) a má tyto složky
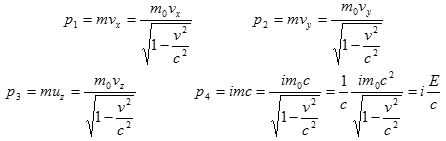
První tři rovnice představují hybnost ve směru os x, y, z.
V klasické mechanice neexistuje přímá souvislost energie tělesa a setrvačné hmotnosti tělesa. Těleso může mít různou pohybovou energii, ale hmotnost tělesa zůstává stále stejná. Ve speciální teorii relativity každá změna energie musí souviset se změnou hmotnosti tělesa. Tuto myšlenku poprvé publikoval Albert Einstein v třístránkovém dodatku s názvem Závisí setrvačnost tělesa na jeho energetickém obsahu?, který vyšel v Annalen der Physik 21. listopadu 1905, tedy dva měsíce po publikování základního článku o speciální teorii relativity. Působí–li na těleso o klidové hmotnosti m0 síla F a uvede těleso z klidu do pohybu, pak se pohybová energie tělesa zvětší o ΔEk, současně se ale zvětší hmotnost tělesa o hodnotu Δm = m – m0. Albert Einstein dokázal, že obecně platí přímá souvislost změny celkové energie a změny hmotnosti tělesa
![]()
Tento vztah platí vždy a nezávisí na způsobu změny energie tělesa. Einstein dále předpokládal, že analogický vztah musí platit také mezi celkovou energií soustavy a její hmotností
![]()
Jestliže se těleso nachází v klidu vzhledem ke zvolené vztažné soustavě, pak říkáme, že má v této soustavě tzv. klidovou energii E0
![]()
Celkovou energii tělesa pak vypočítáme jako součet klidové energie tělesa a pohybové energie tělesa. Pro celkovou energii soustavy platí zákon zachování energie – celková energie izolované soustavy těles zůstává při všech dějích probíhajících uvnitř soustavy konstantní. Zatímco v klasické fyzice jsou zákony zachování hmotnosti a energie dvěma zákony, ve speciální teorii relativity oba zákony splývají díky vztahu mezi energií tělesa a hmotností tělesa.
Ještě můžeme odvodit vztah mezi hybností, energií a klidovou hmotností. K tomu použijeme čtyřvektor hybnosti a tento skalární součin
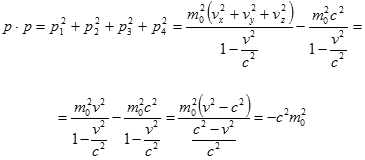
nebo
![]()
Porovnáním obou pravých stran získáme vztah, který se často užívá v kvantové fyzice
![]()
Vyplývá z něj, že můžeme najít také takové stavy, v nichž má částice zápornou energii.
Podle teoretických předpokladů je možné klidovou energii částice plně nebo zcela uvolnit. Tento vztah byl ověřen několika pokusy v jaderné fyzice, poprvé v roce 1932 Johnen Cockroftem a Ernestem Waltonem. Jako důsledek tohoto vztahu můžeme brát i funkci jaderného reaktoru či atomové zbraně nebo urychlovače částic. Díky vztahu pro ekvivalenci energie a hmoty Hans Bethe detailně rozpracoval uhlíko–dusíkový termojaderný cyklus, tedy zdroj energie všech hvězd.
Einsteinův vztah mezi hmotností a energií můžeme použít k výpočtu tzv. hmotnostního úbytku. Klidová hmotnost deuteronu (částice složená z protonu a neutronu) je md = 3,3433 · 10–27 kg; klidová hmotnost protonu a neutronu jsou mp = 1,6726 · 10–27 kg, mn = 1,6749 · 10–27 kg. Jestliže sečteme hmotnosti protonu a neutronu, pak výsledná hmotnost je vyšší než hmotnost deuteria. Rozdíl hmotností se nazývá hmotností úbytek a je to energie potřebná k rozdělení deuteria na proton a neutron (3,8 · 10–13 J).
Je zajímavé, že Einsteinův vzorec mezi energií a hmotností v Einsteinově základní práci Zur Elektrodynamik bewegter Körper nenajdeme. Teprve během léta roku 1905 si Einstein uvědomil tento další důsledek své právě dokončené teorie. Jako dovětek proto sepsal třistránkový článek s názvem Závisí setrvačnost tělesa na jeho energetickém obsahu? Byl odeslán 27. září do Annalen der Physik a vyšel 21. listopadu.
Jen poměrně málo veličin s pohybem nemění svou hodnotu, např. tlak, entropie nebo elektrický náboj.
