Teorie
U člověka se rovnovážné ústrojí nachází stejně jako i u jiných savců ve vnitřním uchu a tvoří ho tři polokruhové chodby a dva váčky. Receptory ve váčcích jsou vláskové buňky uložené v rosolovité hmotě, ve které jsou krystalky uhličitanu vápenatého, které se v ní vlivem gravitace pohybují a naráží na vláskové buňky, ty předávají informace o podráždění pomocí nervů do mozečku. Ten vyhodnocuje informace z obou váčků.
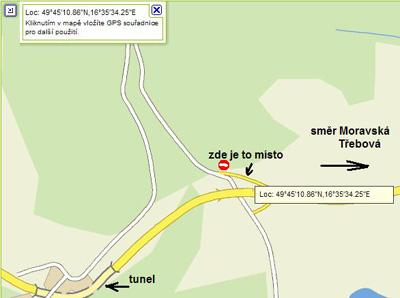
Zmást smysly si můžeme i ve skutečném světě. Příkladem jsou magnetické kopce nebo řeky tekoucí nahoru. Magnetický kopec můžeme najít např. u Moravské Třebové (viz mapa). Na úseku cesty jde silnice z kopce dolů. Můžeme tu vidět auta, jak couvají na neutrál do kopce. Důsledným proměřením nadmořské výšky zjistíme, že je vše v pořádku, jen naše oko cestu považuje za základnu, k níž vztahuje sklon ostatních rovin. Při chůzi nejsme schopni rozeznat sklon 2°– 3°.
Stoupání můžeme měřit pomocí poměru, např. 1:20 znamená, že na každých dvacet metrů se zvedne svah o jeden metr.
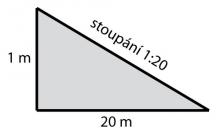
Stoupání/klesání v poměru 1:20.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.Poměr 1:20 je vlastně zlomek 1/20 a zlomky můžeme přepsat jako procentuální podíl z celku. Stačí zlomek upravit tak, aby měl ve jmenovateli číslo 100. Hodnota čitatele pak představuje procenta. Příkladem může být třeba zlomek 1/20 = 5/100 =› 5 %. Znamená to, že na každý metr se kopec zvedne o 5 cm. Pokud není stoupání kopce příliš velké, používají se promile ‰, která představují tisícinu celku, tzn. že zlomek upravíme tak, aby měl ve jmenovateli tisíc.
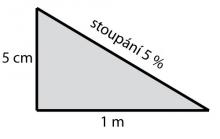
Stoupání/klesání 5 %.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.
Třetí možností zadání stoupání/klesání je použití úhlu. Použijeme goniometrickou funkci tangens v pravoúhlém trojúhelníku, která představuje poměr protilehlé a přilehlé strany k danému úhlu. Pro kopec se stoupáním 1:20 určíme úhel stoupání jako tg α = 1/20, α =› 2,9°.
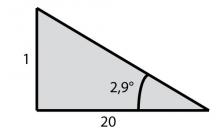
Stoupání/klesání s úhlem 2,9°.
Zdroj: Techmania Science Center. Autor: Magda Králová. Under Creative Commons.